Всем доброго времени суток! Сегодня моя запись о основах цифровой электроники. Но для начало, как говорил один человек, надо определиться с терминологией. То есть, что есть что в цифровой электронике.

Электрический сигнал — это электрическая величина (напряжение, ток), которая изменяется со временем. В основном вся электроника работает с электрическими сигналами, но в последнее время всё чаще используются и другие виды сигналов (например давление, температура, свет).

Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.

Аналоговый сигнал — это сигнал, который может принимать любые значения в определённых пределах (например, напряжение может плавно изменяться в пределах нескольких десятков вольт). Устройства, которые работают только с аналоговыми сигналами, называются аналоговыми устройствами.

Цифровой сигнал — это сигнал, который может принимать только два значения (иногда — три значения). Причём разрешены некоторые отклонения от этих значений. Устройства, которые работают только с цифровыми сигналами, называются цифровыми устройствами.

Достоинство и недостатки аналоговых и цифровых устройств

Изначально все электронные устройства были только лишь аналоговыми, но со временем, когда требования к электронным устройствам выросли, начали проявляться недостатки аналоговой электроники. Всё дело в том, что аналоговые сигналы чувствительны к всяким паразитным воздействиям — шумам, наводкам, помехам, которые искажают полезный сигнал, а при передаче сигнала на большие расстояния они ослабляются.

В отличие от аналоговых сигналов, цифровые, имеющие всего два уровня разрешённых значений, защищены от воздействия шумов, наводок и помех гораздо лучше. Имеющиеся небольшие отклонения от разрешённых значений никак не искажают цифровой сигнал, так как всегда существуют зоны допустимых отклонений. Однако у цифровых устройств имеется крупный недостаток. Дело в том, что для распознавания уровня сигнала необходимо, чтобы этот уровень поддерживался в течении определённого интервала. А аналоговый сигнал может принимать любое значение в течении любого, даже самого минимального, периода времени. Поэтому часто аналоговые сигналы называют непрерывными во времени, а цифровые — дискретные по времени сигналы. Отсюда можно сделать вывод, что максимально достижимое быстродействие аналоговых устройств всегда принципиально выше, чём цифровых.

Математика и электроника

В настоящее время люди умеют считать гораздо лучше, чем в прошлом: у них есть замечательные помощники — умные вычислительные машины. Сегодня вычисления ведутся в сотни тысяч раз быстрее, чем сто лет назад. Как удалось достигнуть этого? Разработчики электронной и компьютерной техники, говорят, что этого достигли тем, что стали считать по другому. Не обязательно считать десятками, сотнями и тысячами ответят они.

Давно известны не десятичные системы счисления, например, система счисления с основанием 12. В роли «десятка» (единицы 2-го разряда) в ней выступает «дюжина», в роли «сотни» (единицы 3-го разряда) — «гросс» (дюжина в квадрате), а единицу четвёртого разряда называют «фут» (дюжина в кубе).

Но в мире цифровой электроники наиболее привлекательными оказались системы счисления с основанием 2, 8 и 16, то есть двоичная, восьмеричная и шестнадцатеричная системы счисления. Наиболее используемая система счисления — это конечно же двоичная. Для этого имеется ряд оснований.

Всякое цифровое устройство должно уметь «читать», «запоминать» и «демонстрировать» цифры и числа, составленные из них. В двоичной системе счисления цифр всего две: 0 и 1.

Легко придумать способ демонстрации двоичных чисел. Двоичное число, например 1001₂, можно записать при помощи гирлянды электрических лампочек: зажжённая лампочка обозначает «1», а не зажжённая — «0». Так изображенное число легко прочитать.

В цифровое устройство двоичное число можно вводить по проводникам электрического тока, например, 5 вольт значит, что демонстрируется «1», а если напряжение равно нулю, то демонстрируется «0».

Для запоминания двоичных чисел используются различные электрические и физические свойства с ярко выраженными двумя состояниями (например, в жёстких дисках используется эффект намагниченности отдельных участков, в оптических дисках — различие в отражающей способности или же на триггерном эффекте когда сама электронная схема хранит информацию).

Второе важное основание для использования двоичной системы — простота двоичной арифметики. Например, таблица сложения будет выглядеть следующим образом:

+	0	1
0	0	1
1	1	10

и таблица умножения

х	0	1
0	0	0
1	0	1

Операции над числами

Как уже упоминалось выше цифровые устройства должно иметь возможность считывать число, запоминать и демонстрировать его. Но для выполнения этих функций не нужно было бы такое разнообразие цифровых устройств. Самое главное что должно уметь выполнять цифровое устройство — это выполнять операции над числами, которые оно принимает на свой вход и на выходе получать какой то результат.

Существует великое множество операций над числами, но в цифровой электронике этих основных операций всего три — это логическое умножение, логическое сложение и логическое отрицание.

1. Логическое умножение (функция «И»). Как же будет зависеть результат на выходе от входных данных? Мы привыкли употреблять союз И так, что слова которые он объединяет понимаются, как неразрывное целое. Например, пусть даны два простых выражения.
Володя принёс молоток — А;
Володя принёс стамеску — В.
Составим их логическое произведение.
Володя принёс молоток И Володя принёс стамеску — (АВ).
Истинным такое высказывание будет только при условии, что Володя принёс оба предмета (А = 1, В = 1). Зависимость истинности логического произведения от сомножителей можно задать таблицей, называемой таблицей истинности:

A	B	AB
1	1	1
1	0	0
0	1	0
0	0	0

2. Логическое сложение (функция «ИЛИ»). Воспользовавшись нашими высказываниями:
<Володя принёс молоток — А;
Володя принёс стамеску — В.
Составим их логическую сумму.
Володя принёс молоток ИЛИ Володя принёс стамеску — (А + В).

Ясно, что ложным такое высказывание будет при условии, что Володя не принёс ни одного из предметов, а истинным когда есть хотя бы один из них. Таблица истинности в таком случае будет следующей:

A	B	A + B
1	1	1
1	0	1
0	1	1
0	0	0

3. Логическое отрицание (функция «НЕ»). Указание совершить операцию отрицания на высказыванием А записывается так: А. Ясно, что если данное высказывание истинно, то его отрицание ложно и наоборот.

Солнце всходит на востоке (А = 1); Солнце не всходит на востоке (А = 0).

Таблица истинности будет такой:

A	А
1	0
0	1

Простейшие логические схемы

Реализацию логических выражений можно осуществить с помощью простых электронных схем, на входы которых поступают электрические входные сигналы, а на выходе формируется выходной сигнал, который соответствует логической функции.

1. Логический элемент И. Представляет собой схему, в которой сигнал 1 на выходе появляется только тогда, когда на входе А и входе В совпадают сигналы 1. Простейший логический элемент И может быть реализован на последовательно включённых контактах реле, управляемых с помощью кнопок.

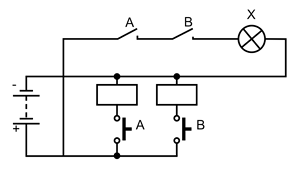
Релейно-контактная схема элемента И

Условное обозначение логического элемента И с двумя входами показано ниже. На выходе логического элемента И сигнал 1 появится только тогда, когда на всех входах совпадут сигналы 1.

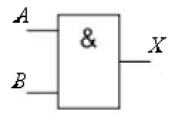
Условное графическое изображение логического элемента И

2. Логический элемент ИЛИ. Представляет собой схему, на выходе которой появляется сигнал 1, если на входе А или входе В или на обоих входах присутствует сигнал 1. Простейший логический элемент ИЛИ может быть реализован на параллельно включённых контактах реле, управляемых с помощью кнопок.

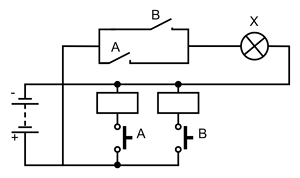
Релейно-контактная схема элемента ИЛИ

Условное обозначение логического элемента ИЛИ с двумя входами показано ниже. На выходе логического элемента ИЛИ сигнал 1 появится в случае появления хотя бы на одном из входов сигнала 1.

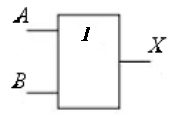
Условное графическое изображение логического элемента ИЛИ

3. Логический элемент НЕ. Представляет собой схему, на выходе А которой появляется сигнал 1 при отсутствии на входе А сигнала 1. Простейший логический элемент НЕ реализован на реле с нормально замкнутыми контактами.

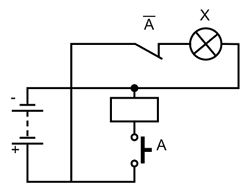
Релейно-контактная схема элемента НЕ

Условное обозначение логического элемента НЕ показано ниже. На выходе логического элемента НЕ сигнал 1 появится в случае отсутствия сигнала 1 на входе

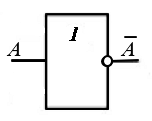
Условное графическое изображение логического элемента НЕ

Логические элементы И, ИЛИ и не предназначены для выполнения трёх основных операций цифровой логики над дискретными сигналами. С помощью этих элементов можно реализовать логические операции любой сложности. Поэтому эти элементы называются основными.