Всем доброго времени суток. Сегодняшний мой пост начинает серию статей про импульсные устройства. Такие устройства предназначены для формирования и преобразования электрических сигналов, имеющих характер импульсов и перепадов напряжений. К импульсным устройствам относятся все цифровые микросхемы и некоторые аналоговые, например, микросхемы генераторов и компараторов. Ранее я рассматривал один из основных элементов импульсных устройств – транзистор, работающий в ключевом режиме.
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
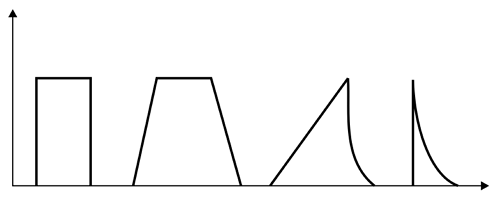
Формы импульса (слева направо): прямоугольная, трапецеидальная, пилообразная, экспоненциальная.
В радиоэлектронике используются импульсы самых разнообразных форм, но наиболее распространённые это: прямоугольные, трапецеидальные, пилообразные и экспоненциальные формы импульсов. Форма любого импульса характеризуется следующими основными параметрами:
- амплитуда (максимальное значение) импульса, Um;
- начальное значение импульса, U0;
- длительность импульса, tи;
- длительность переднего фронта (или просто фронта) импульса, tф;
- длительность заднего фронта (или среза) импульса, tс;
- длительность вершины импульса, tв;
- снижение вершины импульса, Δu;
- крутизна фронта импульса (скорость изменения напряжения при формировании переднего или заднего фронта).
В случае использовании периодичности повторяющихся импульсов имеют большое значение такие параметры, как скважность импульсов (ξ или S), коэффициент заполнения импульсов (η или D), частота повторения импульсов (f) и период повторения импульсов (T). Данные параметры имеют следующие соотношения между собой
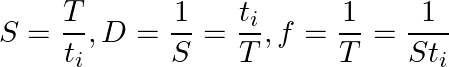
Форма реального импульса
Временные параметры импульса (tи, tф, tс, tв) имеют точное значение только в случае идеального импульса, а в реальности лишь в некоторой степени имеют приближённое значение. Поэтому временные параметры отсчитываются от некоторых приближённых величин, которые в достаточной для практики точности имеют значения 0,05 и 0,95. Поясню на примере формы реального импульса, изображённого выше: при определении длительности фронта (tф) импульса, за начало фронта принимают значение 0,05*Um, а за окончание фронта – 0,95*Um. В случае длительности среза, соответственно, начало – 0,95*Um, а окончание – 0,05*Um.
Переходный процесс
Рассмотрение импульсных устройств и схем не возможно без представлении о переходном процессе. Он возникает в цепях при различных коммутациях, то есть при включении или выключении элементов схемы, источников напряжения, при коротких замыканиях отдельных цепей и т.д. Переходный процесс объясняется тем, что энергия электромагнитных полей, связанных с цепью, в разные промежутки времени неодинакова, а резкое изменение энергии невозможно из-за ограниченной мощности источников питания.
Исходя из вышесказанного, можно сделать вывод, что напряжение на ёмкости и ток в индуктивность не могут изменяться скачкообразно, так как данные параметры определяют энергию электрического поля конденсатора и магнитного поля катушки индуктивности.
Таким образом, можно сделать вывод, что при рассмотрении импульсных схем наибольшее внимание необходимо обратить на цепи, представляющие собой комбинации резисторов и конденсаторов или резисторов и катушек индуктивностей (RC- и RL-цепей). Такие цепи применяются непосредственно для формирования импульсов, а также являются важнейшими элементами релаксационных генераторов, триггеров и других устройств. Поэтому ниже рассмотрим основные свойства элементарных RC- и RL-цепей, а также изменение формы импульсов при прохождении через эти цепи.
Влияние RC- и RL-цепей на импульсы различной формы
Несмотря на то, что формы электрических импульсов довольно разнообразны, их можно представить в виде суммы элементарных (типовых) напряжений трёх форм: скачкообразного, линейно изменяющегося и экспоненциального. Поэтому рассмотрим воздействие различных форм напряжений на RC- и RL-цепи.
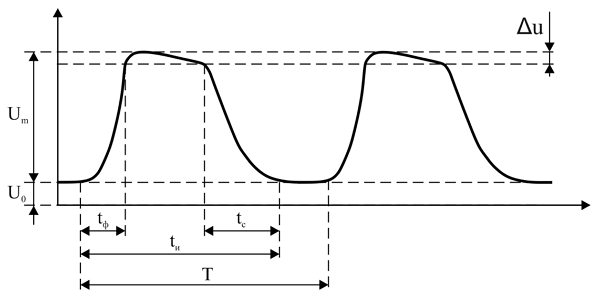
Изображение RC- и RL-цепей.
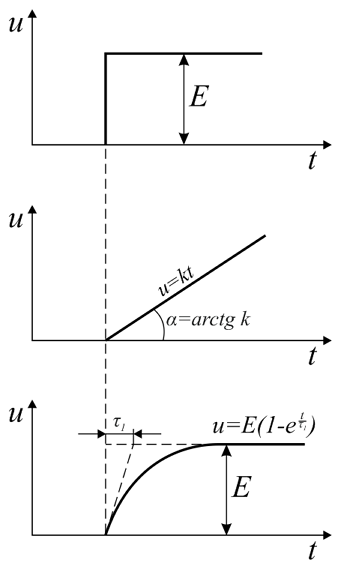
Элементарные формы напряжения (сверху вниз): ступенчатое, линейно-изменяющееся, экспоненциальное.
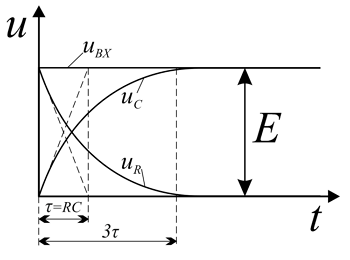
Ступенчатое изменение напряжения. При подключении RC-цепи к источнику постоянного напряжения uвх = Е = const, напряжения на конденсаторе и резисторе будет изменяться по экспоненциальному закону:
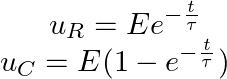
t – время, с;
τ – постоянная времени, с. τ = RC.
С определением напряжения всё понятно, но в практике чаще возникает вопрос о времени установления напряжения. Например, необходимо вычислить время за которое на конденсаторе установится напряжение равное uС = 0,95 Е. Простым преобразованием формулы напряжения получим
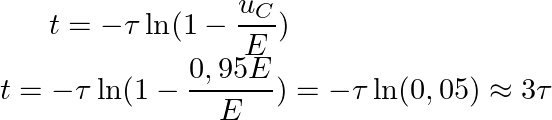
Аналогично при подключении RL-цепи к источнику постоянного напряжения uвх = Е = const
где τ – постоянная времени, с. τ = L/R.
Линейно изменяющееся напряжение. При подключении RC-цепи к источнику линейно изменяющегося напряжения uВХ = kt, напряжения на резисторе и конденсаторе будут изменяться согласно следующей формуле
Для RL-цепи подключённой к источнику с линейно изменяющимся напряжением uВХ = kt, напряжения на элементах соответственно будут такими
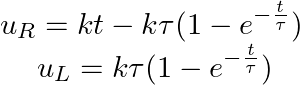
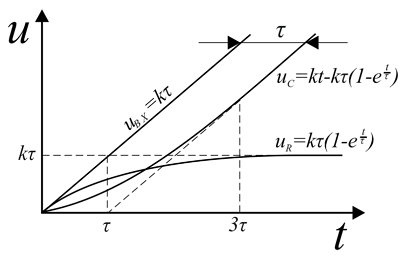
Временные диаграммы напряжений при линейно изменяющемся напряжении в RC- и RL-цепях.
Экспоненциально изменяющееся напряжение. При подключении RC-цепи к источнику экспоненциально изменяющегося напряжения
напряжения на резисторе и конденсаторе будут изменяться согласно следующей формуле
где q = τ/τ1.
Соответственно напряжение на конденсаторе будет равно разности напряжений источника и напряжения на резисторе
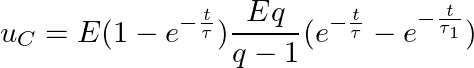
Временные диаграммы для uR представлены ниже при различных значениях q. При больших значениях q, то есть постоянной времени цепи τ, формы напряжений uR близки к формам, соответствующим ступенчатому изменению входного напряжения. При уменьшении τ, кроме сокращения длительности спада напряжения uR, уменьшается и максимальное значение uR.
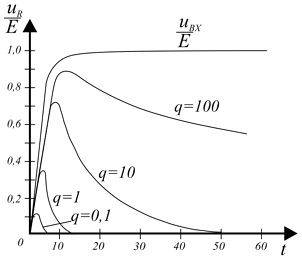
Временные диаграммы напряжений на резисторе RC-цепи при различных значениях
q = τ/τ1.
Формулы и временные диаграммы для напряжений на выходе RL-цепи оказываются такими же, как и для RC-цепи.
Дифференцирующие цепи
Довольно часто в электронике вообще, а в импульсной в частности требуется преобразовать один вид импульсов в другой (например, прямоугольный преобразовать в треугольный). Для этой цели используют различные схемы, в основе которых простейшие RC- и RL-цепи. Такие цепи называются дифференцирующими и интернирующими цепями. Для начала рассмотрим дифференцирующие цепи, которые показаны на изображении ниже.
Своё название дифференцирующие цепи получили от того, что напряжение на выходе такой цепи пропорционально производной входного напряжения, а нахождение производной в математике называется дифференцирование. В случае RC-цепи напряжение снимается с резистора, а в случае RL-цепи – с индуктивности.
Простейшие
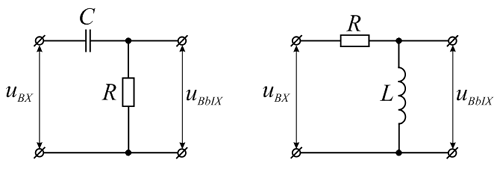 .
.В настоящее время большинство дифференцирующих цепей основаны на RC-цепях, поэтому будем рассматривать их, но все основные выкладки соответствуют также и RL-цепям.
Рассмотрим, как дифференцирующая цепь будет реагировать на прямоугольный импульс. Прямоугольный импульс представляет собой как бы два скачка напряжения. Реакцию RC-цепи на скачкообразное изменение напряжения рассматривалась выше, а в случае прямоугольного импульса выходное напряжение с дифференцирующей цепи будет в виде двух коротких импульсов различной полярности, длительность которых соответствует 3τ = 3RC и 3τ = 3L/R, в случае RL-цепи.
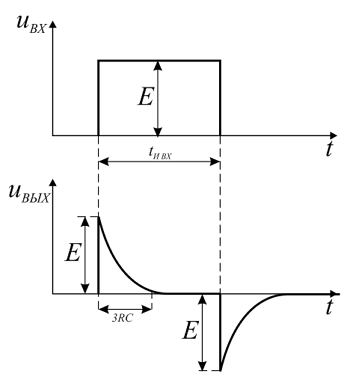
Реакция дифференцирующей цепи на прямоугольный импульс.
Из величины и формы выходного напряжения можно сделать вывод, что дифференциальные цепи вполне могут применяться для уменьшения длительности импульсов, что довольно часто применяется на практике и ранее такие цепи иногда называли укорачивающими.
Интегрирующие цепи
Интегрирующие цепи, так же как и дифференцирующие строят на основе RC- и RL-цепей, отличие заключается в том, откуда снимают выходное напряжение.
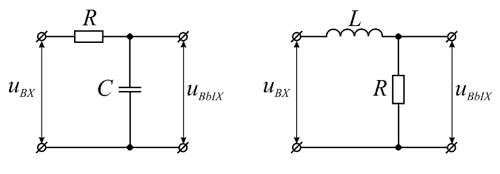
Простейшие RC и RL интегрирующие цепи.
Своё название интегрирующие цепи получили от того, что выходное напряжение, снимаемое с их выхода пропорционально интегралу от входного напряжения. Рассмотрим реакцию интегрирующей цепи на прямоугольный импульс напряжения. Напомню, что прямоугольный импульс, по сути, является напряжением, которое изменяется ступенчато два раза. В результате первого скачка напряжения конденсатор начинает заряжаться до тех пор, пока напряжение на входе не изменится, после этого начнётся разряд конденсатора по экспоненциальному закону.
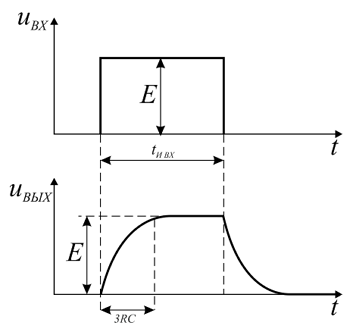
Реакция интегрирующей цепи на прямоугольный импульс.
Не трудно заметить, что длительность импульса на выходе интегрирующей цепи несколько больше, чем длительность импульса на входе. Эту особенность нередко используют для увеличения длительности импульса, и такие цепи ранее называли расширяющими.
Теория это хорошо, но необходимо отрабатывать это всё практически ПОПРОБОВАТЬ МОЖНО ЗДЕСЬ

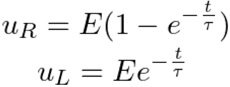
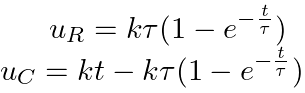
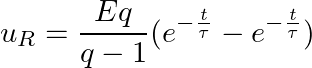
 Генератор пилообразного напряжения. Часть 1
Генератор пилообразного напряжения. Часть 1 Генераторы треугольных импульсов на ОУ
Генераторы треугольных импульсов на ОУ Генераторы пилообразного напряжения. Часть 4. Отрицательная обратная связь
Генераторы пилообразного напряжения. Часть 4. Отрицательная обратная связь Что такое мультивибратор? Расчёт мультивибратора
Что такое мультивибратор? Расчёт мультивибратора Генераторы синусоидальных колебаний на ОУ
Генераторы синусоидальных колебаний на ОУ