Всем доброго времени суток. В прошлых статьях я рассказал о магнитном поле в веществе, а так же магнитных цепях и методах их расчёта. Данная статья посвящена такому явлению, как ЭДС индукции, в каких случаях она возникает, а так же затрону понятие индуктивности, как основного параметра характеризующего возникновение магнитного потока при возникновении электрического поля в проводнике.
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
Как возникает ЭДС индукции и индукционный ток?
Как я говорил в предыдущих статьях вокруг проводника, по которому протекает электрический ток, возникает электромагнитное поле. Данное магнитное поле я рассмотрел здесь и здесь. Однако существует и обратное явление, которое называется электромагнитная индукция. Данное явление открыл английский физик М. Фарадей.
Для рассмотрения данного явления рассмотрим следующий рисунок
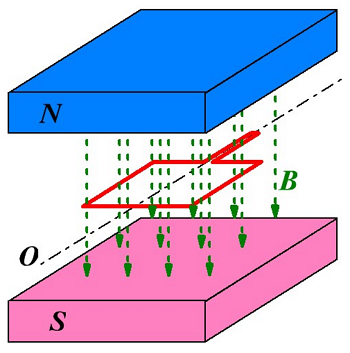
Рисунок, иллюстрирующий электромагнитную индукцию.
На данном рисунке показана рамка из проводника, помещённая в электрическое поле с индукцией В. Если данную рамку двигать вверх-вниз по направлению магнитных силовых линий или влево – вправо перпендикулярно силовым линиям, то магнитный поток Φ пронизывающий рамку буден практически постоянным. Если же вращать рамку вокруг оси О, то за некоторый промежуток времени ∆t магнитный поток изменится на некоторую величину ∆Φ и в результате в рамке появится ЭДС индукции Еi и потечёт ток I, называемым индукционным током.
Чему равно ЭДС индукции?
Для определения величины возникающей ЭДС рассмотрим контур помещенный в однородное магнитное поле с индукцией В, по данному контуру свободно может перемещаться проводник длиной l.
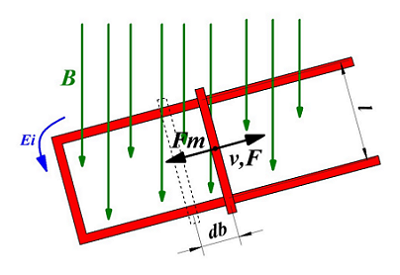
Возникновение ЭДС индукции в прямолинейном проводнике.
Под действием силы F проводник начинает двигаться со скоростью v. За некоторое время ∆t проводник пройдёт путь db. Таким образом, затрачиваемая работа на перемещение проводника составит
![]()
Так как проводник состоит из заряженных частиц – электронов и протонов, то они также движутся вместе с проводником. Как известно на движущуюся заряженную частицу действует сила Лоренца, которая перпендикулярна к направлению движения частицы и к вектору магнитной индукции В, то есть электроны начинают двигаться вдоль проводника приводя к возникновению электрического тока в нём.
Однако на проводник с током в магнитном поле действует некоторая сила Fт, которая в соответствии с правилом левой руки будет противоположна действию силы F, за счёт которой проводник движется. Так как проводник движется равномерно, то есть с постоянной скоростью, то силы Fт и F равны по абсолютному значению
![]()
где В – индукция магнитного поля,
I – сила тока в проводника, возникающая по действием ЭДС индукции,
l – длина проводника.
Так как путь db пройденный проводником зависит от скорости v и времени t, то работа, затрачиваемая на перемещения проводника, в магнитном поле составит
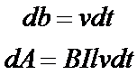
При перемещении проводника в магнитном поле практически вся затрачиваемая на эту работу механическая энергия переходит в электрическую энергию, то есть
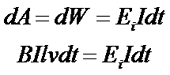
Таким образом, преобразовав последнее выражение, получим значение ЭДС индукции при движении прямолинейного проводника в магнитном поле
![]()
где В – индукция магнитного поля,
l – длина проводника,
v – скорость перемещения проводника.
Данное выражение соответствует движению проводника перпендикулярно линиям магнитной индукции. Если происходит движение под некоторым углом к линиям магнитной индукции, то выражение приобретает вид
![]()
На практике достаточно трудно посчитать скорость перемещения проводника, поэтому преобразуем выражение к следующему виду
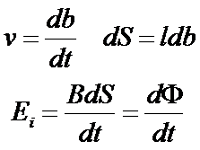
где dS – площадка, которую пересекает проводник при своём движении,
dΦ – магнитный поток пронизывающий площадку dS.
Таким образом, ЭДС индукции равна скорости изменения магнитного потока, который пронизывает контур.
Для обозначения направления движения тока в контуре вводят знак «–», который указывает, что ток в контуре направлен против положительного обхода контура. Таким образом
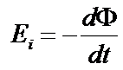
Зачастую в магнитном поле движется контур, состоящий из множества витков провода, поэтому ЭДС индукции будет иметь вид
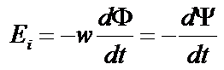
где w – количество витков в контуре,
dΨ = wdΦ – элементарное потокосцепление.
Перефразируя предыдущее определение, ЭДС индукции в контуре равна скорости изменения потокосцепления этого контура.
Что такое ЭДС самоидукции? Индуктивность
Как известно вокруг проводника с током существует магнитное поле. Так как индукция магнитного поля пропорциональна силе тока протекающего через проводник, а магнитный поток пропорционален магнитной индукции, следовательно, магнитный поток пропорционален силе тока, протекающей через проводник.
![]()
Таким образом, при изменении силы тока происходит изменение магнитного потока (или потокосцепления). Однако в соответствие с законом электромагнитной индукции, изменение потокосцепления приводит к возникновению в проводнике ЭДС индукции.
Данное явление (возникновение ЭДС) в проводнике при изменении проходящего по нему тока называется самоиндукцией. Возникающая вследствие самоиндукции ЭДС называется ЭДС самоиндукции ЕL, которая равна
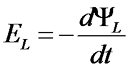
где dΨL – изменение потокосцепления.
Следовательно между электрическим током в проводнике и потокосцеплением, возникающего вокруг проводника магнитного поля существует некоторый коэффициент пропорциональности связывающий их. Таким коэффициентом является индуктивность – обозначается L (имеет старое название коэффициент самоиндукции)
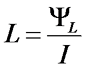
Величина индуктивности характеризует способность электрической цепи создавать потокосцепление (магнитный поток) при протекании по ней электрического тока. Единицей индуктивности является Генри (обозначается Гн)
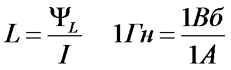
Таким образом, индуктивность зависит от геометрических размеров проводника с током и от магнитных свойств магнитной цепи, через которую замыкается магнитный поток, создаваемый проводником с током.
В следующей статье я расскажу, как рассчитать индуктивность различных по форме проводников с током.
Что такое взаимная индукция? Взаимная индуктивность
Для разъяснения понятия взаимной индукции рассмотрим две катушки К1 и К2 расположенные близко друг от друга
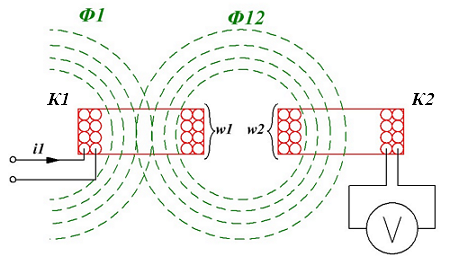
Взаимная индукция двух катушек расположенных рядом.
Если по одной из катушек пропускать электрический ток i1, то вокруг данной катушки возникнет магнитное поле с потоком Φ1, часть магнитных силовых линий которого будет пересекать и вторую катушку, вокруг которой образуется магнитный поток Φ12. Таким образом, при изменении тока i1в первой катушке будет изменяться магнитный поток Φ1, а, следовательно, и магнитный поток Φ12, пересекающий вторую катушку, что непременно приведёт к изменению электрического тока во второй катушке и соответственно возникновению ЭДС.
Таким образом, возникновение ЭДС в контуре под действием изменяющегося тока в близкорасположенном соседней катушке, имеет название взаимной индукции.
Как было сказано выше, явление самоиндукции в количественной форме выражается индуктивностью L, аналогично и взаимная индукция определяется физической величиной называемой взаимной индуктивностью М (имеет размерность Генри – «Гн»). Данная величина определяется отношением потокосцепления во вторичной катушке Ψ12 к току в первичной катушке i1
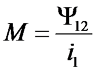
Однако, определить взаимную индукцию можно и обратным способом, то есть пропуская ток i2 через вторичную катушку. В этом случае будет создаваться магнитный поток Φ2, часть которого Φ21 будет пронизывать первичную катушку, тогда взаимная индукция будет определяться следующим выражением
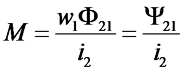
Так же как и в случае с самоиндукцией, ЭДС взаимной индукции во вторичной катушке будет зависеть от скорости изменения магнитного потока или потокосцепления
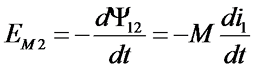
Взаимная индуктивность М имеет зависимость от индуктивности двух катушек и определяется согласно следующему выражению
![]()
где k – коэффициент связи, зависящий от степени индуктивной связи между катушками;
L1 – индуктивность первой катушки;
L2 – индуктивность второй катушки.
Коэффициент индуктивной связи k определяется следующим выражением
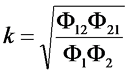
Из данного выражения видно, что коэффициент связи всегда будет меньше единицы, так как Φ12< Φ1 и Φ21< Φ2.
Теория это хорошо, но необходимо отрабатывать это всё практически ПОПРОБОВАТЬ МОЖНО ЗДЕСЬ
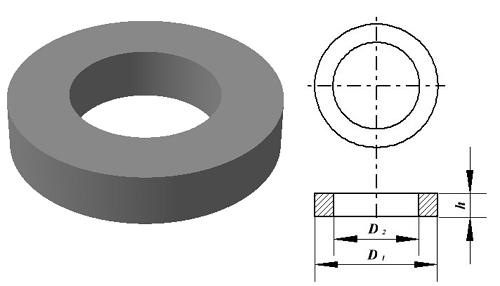 Как рассчитать индуктивность катушек с замкнутыми сердечниками?
Как рассчитать индуктивность катушек с замкнутыми сердечниками? Типы полупроводниковых диодов
Типы полупроводниковых диодов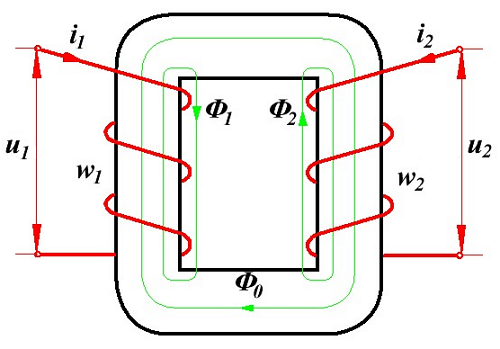 Устройство и схема трансформатора
Устройство и схема трансформатора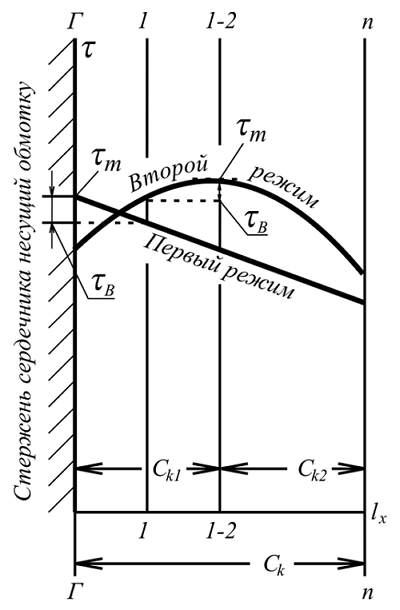 Тепловой режим трансформатора. Часть 1
Тепловой режим трансформатора. Часть 1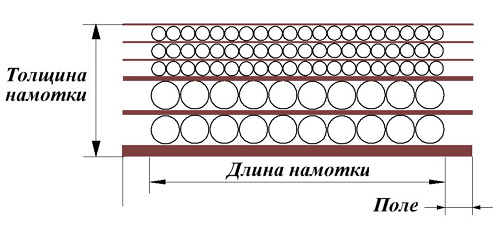 Как определить размеры трансформатора?
Как определить размеры трансформатора?