Всем доброго времени суток! В прошедших статьях я рассказывал о расчёте индуктивности катушек без сердечников и катушек с замкнутыми сердечниками. Сегодняшняя статья посвящена катушкам индуктивности на разомкнутых сердечниках. Такие сердечники можно разделить на два типа: сердечники с малым зазором (δ << a), где δ – величина зазора намного меньше а – любого линейного размера сердечника и сердечники с большим зазором (δ ≥ а), где величина воздушного зазора δ больше или сопоставима с линейными размерами сердечника а. Вначале разберём сердечники с малыми зазорами.
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
Особенности расчёта катушек индуктивности с малыми воздушными зазорами
Разделение сердечников на два типа, с малым и большим зазором, определяется методами расчёта катушек индуктивности на таких типах магнитопроводах.
Для магнитопроводов имеющих малый зазор полностью применяются все формулы для расчёта катушек индуктивности на замкнутых сердечниках. Но для учёта малого зазора в выражениях заменяют параметр относительной магнитной проницаемости вещества μr на параметр эквивалентной магнитной проницаемости сердечника с зазором μе, тогда выражение для индуктивности катушки будет иметь вид
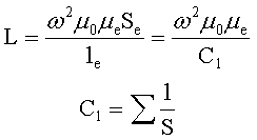
где ω – количество витков катушки,
μ0 – магнитная постоянная, μ0 = 4π*10-7,
μе – эквивалентная магнитная проницаемость сердечника с зазором,
Se – эффективная площадь поперечного сечения сердечника,
le – эффективный путь магнитной линии сердечника,
С1 – первая постоянная сердечника,
l – длина линейного или углового участка сердечника,
S – площадь сечения линейного или углового участка сердечника.
Параметры le, Se и С1 можно определить методами, которые изложены в предыдущих статьях (часть 1 и часть 2) или в документации на сердечник.
При расчёте эффективной проницаемости сердечников с малыми зазорами вводят предположение, что индуктивность рассеивания пренебрежимо мала по сравнению с рабочей индуктивностью, при этом сечение зазора принимается равным сечению полюсов сердечника, а длина магнитного зазора равна расстоянию между полюсами сердечника.
Как определить эффективную магнитную проницаемость сердечника с зазором
Эффективная магнитная проницаемость сердечника с зазором μе связанная c таким понятием, как сопротивление магнитному потоку Rm, которое имеет сходство с электрическим сопротивлением в том плане, что зависит от длины и сечения магнитопровода (электросопротивление зависит от длины и сечения электрического проводника). Сопротивление магнитному потоку определяется следующим выражением
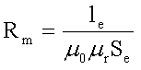
Из данного выражения можно сделать вывод, что чем меньше магнитная проницаемость материала, тем выше магнитное сопротивление. Не трудно заметить, что с учетом относительной магнитной проницаемости вещества сердечника (порядка нескольких тысяч) и воздуха (примерно равно единице), магнитное сопротивление сердечника с зазором будет, в значительной степени, определятся размерами воздушного зазора.
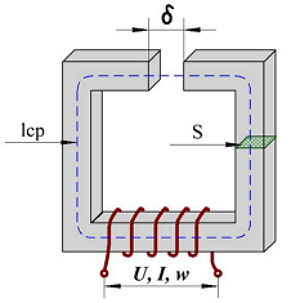
Магнитная цепь магнитопровода с воздушным зазором.
Таким образом, полное магнитное сопротивление сердечника с зазором RO будет состоять из последовательных магнитных сопротивлений сердечника RC и магнитного сопротивления зазора RЗ. С учётом того что относительная магнитная проницаемость воздуха примерно равна единице μr = 1, то получим следующее выражение
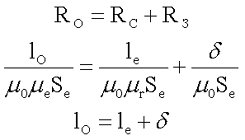
где μ0 – магнитная постоянная, μ0 = 4π*10-7,
μе – эквивалентная магнитная проницаемость сердечника с зазором,
μr – абсолютная магнитная проницаемость вещества сердечника,
Se – эффективная площадь поперечного сечения сердечника,
le – эффективный путь магнитной линии сердечника,
l0 – длина магнитной силовой линии сердечника с зазором,
δ – длина воздушного зазора.
После преобразования получим
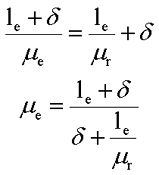
Так как длина зазора меньше чем длина магнитной линии сердечника (δ << le), то из данного выражения можно получить выражение для эффективной магнитной проницаемости сердечника с зазором
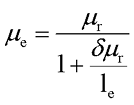
где μе – эквивалентная магнитная проницаемость сердечника с зазором,
μr – абсолютная магнитная проницаемость вещества сердечника,
le – эффективный путь магнитной линии сердечника,
δ – длина воздушного зазора.
Данное выражение показывает, что эффективная магнитная проницаемость сердечника с зазором, а, следовательно, и индуктивность катушки про прочих постоянных параметрах уменьшается при увеличении величины зазора.
Расчёт индуктивности сердечников с малым воздушным зазором
В начале рассмотрим катушки индуктивности, сердечники которых имеют величину воздушного зазора меньше линейных размеров сердечника δ << a.
В качестве примера рассчитаем индуктивность катушки намотанной на сердечнике типа Ш20х28, магнитная проницаемость сердечника составляет μr = 2000. Эффективные параметры сердечника составляют: длина le ≈ 144,5 мм = 0,1445 м, площадь Se ≈ 574,4 мм2 = 5,744*10-4 м2. В сердечнике создан воздушный зазор длиной δ = 0,5 мм. Определим индуктивность катушки состоящей из w = 50 витков с воздушным зазором и без зазора.
1. Определим индуктивность катушки без зазора
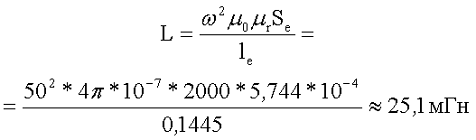
2. Определим индуктивность катушки с зазором
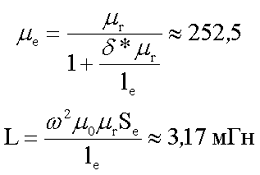
Как видно из получившихся результатов введение столь малого зазора в сердечник уменьшает индуктивность данной катушки более чем в 8 раз.
Теория это хорошо, но необходимо отрабатывать это всё практически ПОПРОБОВАТЬ МОЖНО ЗДЕСЬ
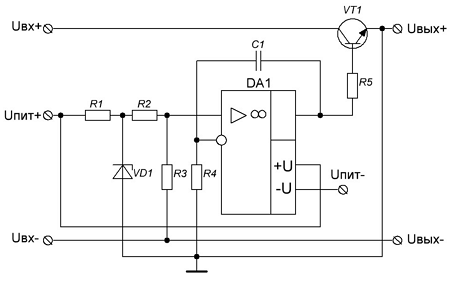 Высоковольтный стабилизатор на ОУ
Высоковольтный стабилизатор на ОУ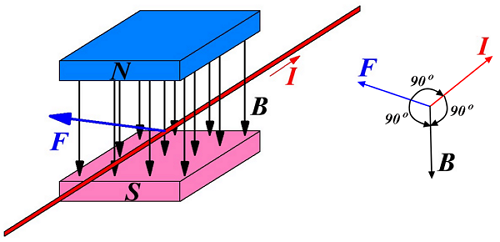 Электромагнетизм. Введение
Электромагнетизм. Введение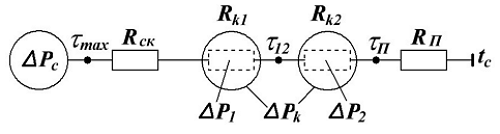 Тепловой режим трансформатора. Часть 2
Тепловой режим трансформатора. Часть 2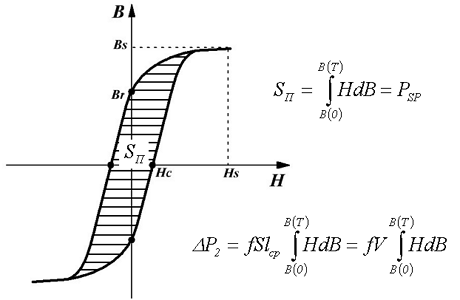 Потери мощности в дросселе. Часть 2
Потери мощности в дросселе. Часть 2 Пример расчёта сердечника трансформатора
Пример расчёта сердечника трансформатора