Всем доброго времени суток! В прошлой статье я начал рассказывать о параметрах трансформатора: мощности, токе намагничивания и падении напряжения. Сегодня продолжим и поговорим о таких важных электромагнитных параметрах, как плотность тока в обмотках трансформатора и магнитная индукция в сердечнике. Также я покажу, как их определить с достаточной для инженерной практики точности.
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
Влияние на параметры трансформатора тепловых режимов
В статьях о тепловых режимах трансформатора, я указывал, что существует два различных тепловых режима трансформатора. Как будет показано ниже, от типа теплового режима трансформатора принципиальным образом зависят электромагнитные параметры трансформатора.
Тепловой режим трансформатора (перегрев) напрямую зависит от потерь мощности в трансформаторе ∆Р и его составляющих: потерь в сердечнике ∆рс и потерь в катушке ∆рк. Режим работы, при котором получается максимальный КПД у данного трансформатора, характеризуется равенством потерь в сердечнике и в катушке, то есть соотношение потерь равно ν = 1
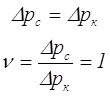
где – соотношение потерь в трансформаторе.
Данный режим работы считается базовым, но не всегда оптимальным. Известно, что для трансформатора с открытым сердечником тепловой режим при ν > 1 (потери в сердечнике выше) более благоприятен, чем при ν < 1 (потери в катушке выше). То есть существует некоторое оптимальное соотношение потерь в сердечнике и в катушке, при которых достигаются наилучшие показатели трансформатора (ν = νо).
Режим работы трансформатора, при котором соотношение потерь не меньше оптимальных (ν ≥ νо), называется естественным, а трансформаторы соответственно естественного режима работы (ТЕР). Но иногда этого достичь затруднительно, из-за возможных ограничений на потери в сердечнике или в катушке. Поэтому в противоположность естественным режимам работы, трансформаторы работают при вынужденных тепловых режимах (ν < νо), а трансформаторы, работающие в этих режимах – вынужденного режима работы (ТВР).
В трансформаторах естественного режима работы величина магнитной индукции В полностью зависит от теплового режима (потерями в сердечнике), то есть она всегда будет меньше индукции насыщения (В < Bs). Для трансформаторов вынужденного режима работы выбор индукции ограничивается условиями намагничивания, то есть она ограниченна индукцией насыщения (В = Bs).
Чаще всего к ТВР относятся трансформаторы нормальной (промышленной) частоты, кроме трансформаторов, рассчитываемых на заданной падение напряжения; маленькие трансформаторы повышенной частоты (до 500 Гц); трансформаторы с высоким перегревом; трансформаторы повторно-кратковременного режима работы, если qp >> 1. К трансформаторам ТЕР, как правило, относятся трансформаторы повышенной и высокой частоты и трансформаторы нормальной частоты (кроме малых) с очень низким перегревом.
Для обычных условий ТВР – это трансформаторы в большинстве своём нормальной (промышленной) частоты, а ТЕР – трансформаторы повышенной и высокой частоты.
Если в ходе расчета ТВР было получено ν > νо, то данный трансформатор ошибочно отнесён к категории ТВР и его необходимо рассчитывать, как ТЕР. Если при расчёте ТЕР было получено В >Bs, то такой трансформатор необходимо пересчитать как ТВР.
Рассмотрим, как определить оптимальное соотношение потерь νо в трансформаторе.
Как определить соотношение потерь в трансформаторе?
Рассмотрим вначале выражения для трансформаторов естественного режима (ТЕР). В качестве основного критерия для нахождения оптимального соотношения потерь мощности в трансформаторе νо, в данном случае, считается получение максимальной мощности Р у данного трансформатора при заданном значении перегрева. Для нахождения ответа на этот вопрос необходимо решить уравнение вида ∆Р/∆ν = 0. Где мощность Р определяется довольно громоздким выражением, но если опустить не зависящие от ν постоянные, то уравнение будет иметь следующий вид
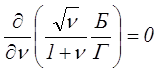
где Б – параметр, характеризующий роль сердечника в охлаждении трансформатора,
Γ – коэффициент перепада температур внутри катушки.
В первом приближении Б/Г = const, тогда решением уравнения будет
![]()
Таким образом, первым критерием оптимальности режима работы является ν0 = 1. Однако для различных типов трансформаторов отношение Б/Г ≠ const. Раскроем истинное значение Б/Г для этих трансформаторов. Так как параметр Б определяется следующим выражением
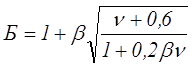
где β – отношение поверхностей охлаждения сердечника и катушки.
Тогда для тороидального трансформатора (ТТ) β = 0, Б = 1, Г – определяется следующим выражением
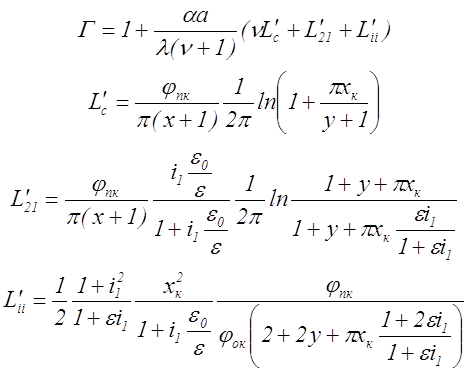
где α – коэффициент теплоотдачи трансформатора,
λ – коэффициент теплопроводности трансформатора,
а – базовый параметр трансформатора,
L/ii – функциональные зависимости температурного перегрева трансформатора для внутренних перегревов τii.
φпк – функция площади поверхности трансформатора
φок – функция площади сечения окна трансформатора
i1 – относительный ток первичной обмотки
ε – отношение плотностей токов вторичной и первичной обмоток, ε = j2/j1,
ε0 – оптимальное значение ε.
Подставляя в уравнение выражения для Б и Γ получаем следующий результат
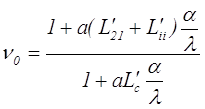
В соответствие с выражениями для Γ (L/21 + L/ii) < L/c и как следствие νо < 1. Кроме того видно, что значение оптимального соотношения потерь мощности νо тем меньше, чем больше размеры тороидального трансформатора и чем больше соотношение α/λ. Для примера, приведены некоторые значения νо для тороидального трансформатора при большом значении х = 3 и различных значениях а.
| а, см | 0,5 | 1 | 2 | 4 |
| νо при λ = 3*10-3 | 0,96 | 0,95 | 0,92 | 0,88 |
| νо при λ = 1*10-3 | 0,92 | 0,91 | 0,88 | 0,84 |
Таким образом, величину отношения потерь ν для трансформатора с закрытым сердечником (ТТ) можно выбирать в диапазоне
![]()
где ν0 определяется предыдущим выражением.
Для трансформаторов с открытым сердечником (броневые и стержневые) выражение для оптимального соотношения потерь будет иметь другой вид. Так как β > 0, коэффициент перепада температур Γ очень близок к 1, Б определяется общим выражением. Тогда уравнение оптимальности будет иметь следующий вид
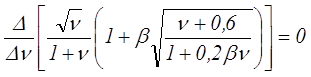
Однако данное уравнение в общем виде неразрешимо, поэтому ограничимся зоной практических значений 0 ≤ β ≤ 5, тогда коэффициент νо будет определяться выражением
![]()
И для типовых условий
![]()
Так как в указанном диапазоне β – 0,2β2 > 0, то νо > 1, то значение отношения потерь в трансформаторе будет лежать в диапазоне
![]()
Из полученных условий можно сделать вывод, что в случае если отсутствуют точные данные об оптимальном значении νо, то для начала расчетов можно считать равным базовому значению ν = 1.
Как определить электромагнитные нагрузки трансформатора?
К важнейшим параметрам трансформатора относятся плотность тока j в обмотках трансформатора и магнитная индукция В в его сердечнике. Существует несколько способов определения данных параметров в зависимости от наличия тех и иных параметров. Рассмотрим общий случай определения плотности тока j и индукции B, когда размеры сердечника и трансформатора неизвестны, а установлена только габаритная мощность РГ требуемого трансформатора.
Плотность тока и магнитная индукция кроме габаритной мощности зависит от геометрических функций трансформатора (подробнее здесь), частоты переменного тока f и режима работы (постоянный или повторно-кратковременный) qp. Кроме этого существенное влияние оказывает тепловой режим работы трансформатора: ТВР или ТЕР. В зависимости от этого электромагнитные нагрузки определяются следующими выражениями.
Для трансформатора вынужденного режима (ТВР):
— заданы ограничения по падению напряжения u = const
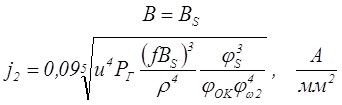
где u – относительное падение напряжения,
РГ – габаритная мощность трансформатора, Вт,
f – частота переменного напряжения, Гц,
BS – максимальное значение рабочей индукции в сердечнике, Тл,
ρ – удельное сопротивление проводникового материала. Для первоначального расчёта берётся при температуре t = 20 ºC, для меди ρ = 0,0175 Ом*мм2/м, для алюминия – 0,028 Ом*мм2/м,
φi – функции геометрии выбранного сердечника.
— заданны ограничения по перегреву трансформатора τ = const
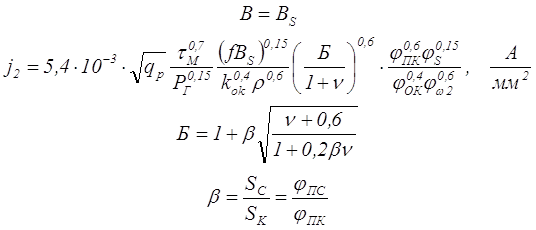
где qP – коэффициент допустимого увеличения потерь в повторно-кратковременном режиме работы трансформатора, при продолжительной работе qP = 1,
τМ – максимальный перегрев трансформатора, ºС
РГ – габаритная мощность трансформатора, Вт,
f – частота переменного напряжения, Гц,
BS – максимальное значение рабочей индукции в сердечнике, Тл,
ρ – удельное сопротивление проводникового материала. Для первоначального расчёта берётся при температуре t = 20 ºC, для меди ρ = 0,0175 Ом*мм2/м, для алюминия – 0,028 Ом*мм2/м,
Б – расчётный параметр для определения перегрева,
β – отношение площадей поверхности охлаждения сердечника и катушки,
ν – соотношение потерь в сердечнике и катушке,
φi – функции геометрии выбранного сердечника.
Для трансформатора естественного режима (ТЕР):
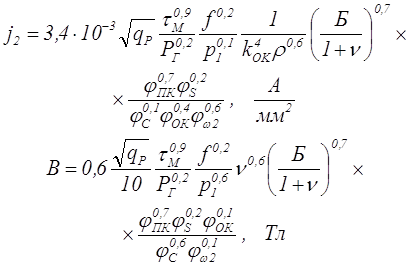
где p1 – удельные потери в сердечнике, Вт/кг.
Замечу, что формулы приведены для плотности тока вторичной обмотки j2; плотность в первичной обмотке j1 и средняя плотность будут выше, в соответствии с выражением ε = j2/j1.
Теория это хорошо, но необходимо отрабатывать это всё практически ПОПРОБОВАТЬ МОЖНО ЗДЕСЬ
 Как рассчитать индуктивность катушек с замкнутыми сердечниками?
Как рассчитать индуктивность катушек с замкнутыми сердечниками? Как рассчитать индуктивность катушек с замкнутыми сердечниками? Часть 2.
Как рассчитать индуктивность катушек с замкнутыми сердечниками? Часть 2. Пример расчёта сердечника трансформатора
Пример расчёта сердечника трансформатора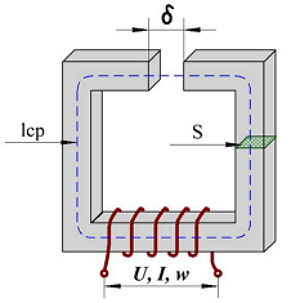 Катушки индуктивности с малым воздушным зазором
Катушки индуктивности с малым воздушным зазором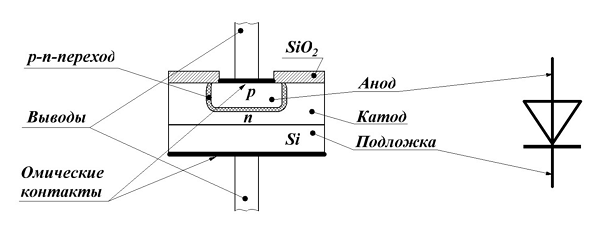 Устройство и параметры диода
Устройство и параметры диода