Всем доброго времени суток! В прошлой статье я рассказал об эквивалентной схеме трансформатора. В данной статье я расскажу, как рассчитать потери мощности в трансформаторе. От потерь мощности в трансформаторе зависит температура его нагрева, поэтому они значительно влияют на расчётные параметры. При расчёте трансформатора следует ограничивать потери мощности путем правильного выбора параметров и величин, влияющих на потери.

Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.

Составляющие потерь мощности в трансформаторе

Полные или суммарные потери мощности в трансформаторе ∆р состоят в основном из двух частей: потерь в сердечнике ∆р_с и потерь в катушках ∆р_к. Присутствующие потери мощности в элементах конструкций трансформатора имеют достаточно малое значение и обычно не учитываются.

При расчёте трансформатора, кроме вышеназванных величин, важное значение имеет соотношение потерь мощности ν и отношение суммарных потерь мощности ∆р к выходной мощности Р₂, называемое коэффициентом потерь k_пот

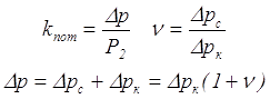
Довольно часто потери мощности ∆р_с и ∆р_к называют потерями «в стали» и потерями «в меди», однако это не совсем правильно, так как в качестве материала сердечника используются не только стали, но и различные сплавов, а в качестве материала проводов обмоток – не только медные, но и алюминий.

Потери мощности в катушках ∆р_к, кроме основной части – потерь в обмотках – включает в себя потери в диэлектрике: изоляции проводника, межслоевой и межобмоточной ∆р_д. Однако, данный компонент потерь мощности начинает влиять на общие потери, только у высоковольтных высокочастотных трансформаторов. Рассмотрим составляющие потерь мощности трансформатора.

Потери мощности в сердечнике трансформатора

В сердечнике ∆р_с трансформатора потери мощности обусловлены затратами энергии магнитного поля на перемагничивание материала из которого сделан сердечник.

Энергия магнитного поля в общем случае определяется следующим выражением

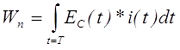
где E_C(t) – изменение напряжения за один период,

i(t) – изменение тока за один период.

В соответствие с законом электромагнитной индукции и теоремой о циркуляции вектора напряженности магнитного поля получим

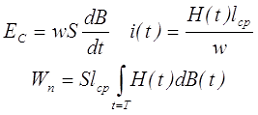
где S – площадь поперечного сечения магнитопровода,

l_cp – средняя длина магнитной силовой линии.

Так как ферромагнитные сердечники обладают гистерезисом, то однозначной функциональной зависимости между напряженностью Н и индукцией В магнитного поля в нем не существует. Однако при перемагничивании сердечника от –Н_max до Н_max можно считать, что любой величине напряженности магнитного поля Н соответствует только два значения магнитной индукции В: на восходящей и нисходящей ветвях. То есть, после полного цикла перемагничивания ферромагнетик вернётся в тоже состояние, из которого начинался процесс. Тогда подынтегральное выражение имеет физический смысл теплоты, отданной сердечником за один цикл перемегничивания.

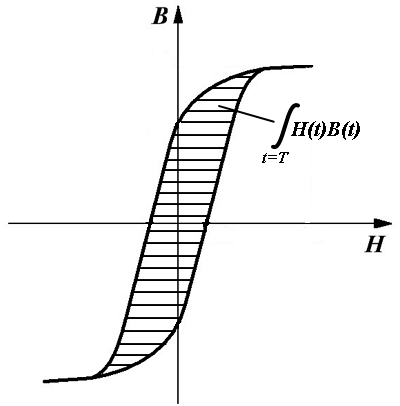
Физический смысл магнитных потерь в сердечнике.

Так как потери мощности в сердечнике ∆р_с определяется, как работа за единицу времени, то преобразовав предыдущую формулу, получим выражение для вычисления потерь мощности в сердечнике

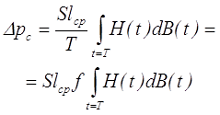
где f – частота перемагничивания магнитопровода.

Подынтегральное выражение численно равно площади заштрихованного участка петли гистерезиса. Таким образом, вычисление данного интеграла является вычислением удельных потерь.

На практике нет необходимости в вычислении удельных потерь, так как для разработанных ферромагнитных материалов существуют справочные данные. Поэтому используют различные формулы в зависимости от известных справочных данных.

Достаточно широко распространено следующее выражение для высокочастотных материалов, где удельные потери имеют размерность Вт/(см³Гц)

P_SV – удельные объемные потери в магнитопроводе,

V_e – эквивалентный объем сердечника магнитопровода,

f – частота перемагничивания.

Так для отечественных ферритов значение удельных объемных потерь составляют

Марка феррита	PSV, мкВт/(см3*Гц), на частоте 10-20кГц			При индукции В, Тл
	Т, °С
	+25	+100	+120
2500НМС1	10,5	8,7	—	0,2
2500НМС2	8,5	6	—	0,2
2500НМС5	9,0	7,6	—	0,2 (при 100 кГц)
3000НМС	2,5	—	2,5	0,1

Кроме данного выражения существуют более сложные способы вычисления потерь мощности в сердечнике трансформатора. Часто в справочниках приводятся удельные объемные потери P_SV в Вт/см³ или удельные массовые потери P_SM в Вт/кг. В этом случае потери мощности рассчитываются по следующим выражениям

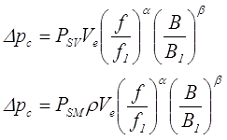
где ρ – плотность материала,

f₁, B₁ – базовые расчётные параметры, при которых были измерены потери мощности в сердечнике,

α и β – степенные параметры, зависящие от конкретного материала, их значение можно найти в справочниках.

Материал	PSV Вт/см3	α	β
2000НМ-А	0,142	1,2	2,4
2000НМ-17	0,272	1,2	2,8
3000НМ-А	0,208	1,2	2,8
1500НМ3	0,093	1,2	2,2
2000НМ3	0,178	1,3	2,7

Для данных материалов В₁ = 1 Тл, f₁ = 1 кГц.

 

Материал	Толщина, мм	PSM, Вт/кг	α	β
34НКМП	0,1	2,2	1,65	1,7
40НКМП	0,05	2,8	1,5	1,3
50НП	0,1	5	1,4	1,5
79НМ	0,1	1,4	1,65	2,0
68НМП	0,05	2,2	1,55	1,7
80НХС	0,05	1,2	1,5	2,0

Для данных материалов В₁ = 0,5 Тл, f₁ = 1 кГц.

Для ферритов иностранного производства выпускаются довольно подробные справочные материалы. Для расчета потерь в сердечниках из этих ферритов используется коэффициент удельных объемных потерь P_V (Relative core losses) измеряемый в кВт/м³. Для этого параметра приводятся подробные графические зависимости от частоты f, магнитной индукции В и температуры Т.

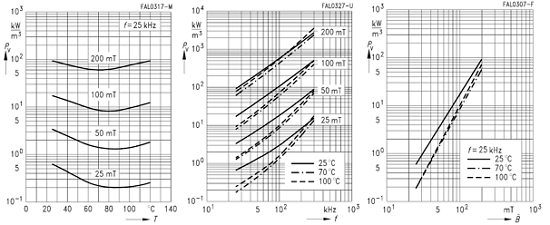
Зависимость удельных потерь P_V для феррита N72 от различных параметров.

Поэтому для нахождения потерь мощности для сердечников из таких материалов достаточно воспользоваться следующим выражением

где P_V – удельные объемные потери в конкретных условиях,

V_e – эффективный объем сердечника.

Как рассчитать потери мощности в наборных сердечниках?

Удельные потери магнитного материала в наборных сердечниках превышают аналогичные у прессованных. Причиной увеличения потерь является негативное влияние технологических операций при изготовлении сердечников. Для учета данного влияния вводят коэффициент увеличения потерь k_p:

где Р_сн – удельные потери мощности в наборном (ленточном или шихтованном) сердечнике,

Р_V^/ – удельные потери материала, из которого изготовлены пластины или ленты сердечника,

k_p – коэффициент увеличения потерь.

Значения данного коэффициента зависят от технологии изготовления, вида материала, рабочей частоты и вида сердечника. Так для наборных сердечников (ЛС и ШС) из электротехнической стали определяется следующим выражением

А для разрезных ленточных сердечников из железоникелевых сплавов

где ψ_а – параметр учитывающий тип сердечника. Для разъёмных сердечников (СТ, БТ) ψ_а = 3, а для замкнутых (ТТ) составляет ψ_а = 1.

В таблице ниже приведены типовые значения коэффициента увеличения потерь

Тип сердечника	Материал		Значения kp при частоте в Гц
	Вид	Толщина	50	400	2000	10000
ШС и замкнутые ЛС	Стали и сплавы	0,15-0,35	1,15	1,2	1,25	1,3
		0,05	—	1,25	1,35	1,4
Разрезные ЛС	Эл. тех. стали	0,15-0,35	1,3	1,4	1,5	1,6
		0,05	—	1,5	1,6	1,7
	50Н, 33НКМС	0,05-0,1	—	1,7	1,8	1,9
	80НХС, 79НМ	0,05-0,1	—	2,5	2,8	3

Значение коэффициента добавочных потерь k_p даны для сердечников средних размеров (несколько десятков Вт). Для сердечников меньших размеров значение данного коэффициента необходимо увеличить в 1,2 – 1,3 раза, а для больших сердечников уменьшить в 1,2 – 1,3 раза.

Как рассчитать потери мощности в обмотках трансформатора?

Потери мощности в обмотках трансформатора ∆р_к напрямую зависят от их активного сопротивления R_i. Кроме того необходимо учитывать увеличение сопротивления из-за дополнительных факторов (увеличение температуры и скин-эффект). В общем случае потери мощности в обмотках определяются следующим выражением

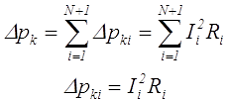
где N – количество вторичных обмоток,

р_ki – потери в i-й обмотке,

I_i – сила тока в i-й обмотке,

R_i – сопротивление i-й обмотки.

Сопротивление обмотки рассчитывается по известной формуле, через удельное сопротивление

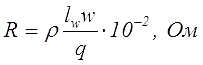
где l_w – средняя длина витка обмотки, см,

w – число витков обмотки,

q – сечение проводника, мм²,

ρ – удельное сопротивление материала проводника, Ом*мм²/м.

Данное выражение достаточно неудобно использовать на практике. Чаще всего известны размеры сердечника, а также его основные параметры (площади и объёмы). Поэтому можно использовать следующее выражение для потерь мощности в обмотках трансформатора

где k_oki – коэффициент заполнения окна для i-й обмотки,

V_ki – геометрический объем, занятый i-й обмоткой, см³,

j_i – плотность тока для i-й обмотки, а/мм²,

S_oki – площадь сечения i-й обмотки, мм²,

Если параметры ρ, j, k_ok одинаковы для всех обмоток либо взяты их средние значения, то получим следующее выражение

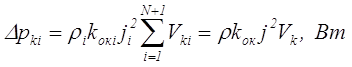
где V_k – геометрический объем, занятый всей катушкой, см³.

Как уже было сказано, при работе трансформатор нагревается. Вместе с этим изменяется активное сопротивление обмоток. Рассчитать удельное сопротивление проводника при увеличении температуры можно по следующим выражениям

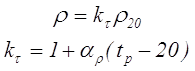
где k_τ — коэффициент учитывающий увеличение сопротивления из-за роста температуры,

ρ₂₀ – удельное сопротивление проводника при температуре 20°С,

α_ρ – температурный коэффициент сопротивления, для меди и алюминия α_ρ = 0,004 1/°С,

t_p – рабочая температура трансформатора, °С.

Так как в большинстве случаев в справочниках указывают удельное сопротивление материалов при температуре 20°С, то выражение можно упростить

где τ – перегрев трансформатора.

Влияние температуры на сопротивление обмотки трансформатора необходимо всегда учитывать при расчете падения напряжения на них.

Как влияет переменное напряжение на потери мощности в обмотках?

При протекании переменного электрического тока по проводнику возбуждаются вихревые токи или токи Фуко. Они направленны так, что ослабляют ток внутри провода и усиливают вблизи поверхности. В результате переменный ток оказывается неравномерно распределённым по сечению провода – он как бы вытесняется на поверхность проводника. Данное явление называется скин-эффектом или поверхностным эффектом.

Вследствие этого эффекта плотность тока у поверхности проводника максимальна, а на глубине ∆ становится меньше в е раз (примерно на 70%). Глубину скин-слоя можно определить по следующему выражению

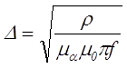
где ρ – удельное сопротивление проводника, для меди ρ = 0,0172 Ом*мм²/м,

μ_α — абсолютная магнитная проницаемость проводника,  для меди μ_α = 4*π*10^-7 Гн/м,

μ₀ — относительная магнитная проницаемость проводника,  для меди μ₀ ≈ 1,

f – частота переменного тока.

Кроме скин-эффекта в проводниках, в обмотках трансформатора, проявляется так называемый катушечный эффект и эффект близости проводников, заключающегося в том что переменное напряжение за счет токов Фуко вытесняется во внешнюю часть обмотки. Данные эффекты также увеличивают сопротивление обмотки трансформатора. Для учета данный факторов вводят поправочный коэффициент k_f

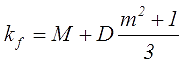
где m – число слоёв в обмотке.

Для определения коэффициентов M и D необходимо воспользоваться следующими выражениями

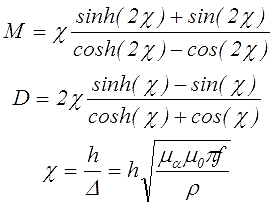
где χ – высота одного слоя обмотки, отнесённая к глубине скин-слоя,

∆ — глубина скин-слоя,

h – высота проводника,

sinh и cosh – гиперболические синус и косинус, соответственно.

Высота проводника h не эквивалентна его диаметру d. Только если производится намотка фольгой, параметр высота проводника h равен толщине фольги, в случае круглого провода высота проводника h равна

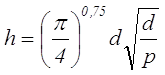
где d – диаметр проводника,

р – расстояние между центрами соседних проводников.

При использовании многожильного обмоточного провода (литцендрата), выражение для поправочного коэффициента k_f будет иметь следующий вид

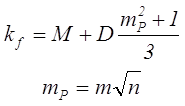
где m_Р – приведённое количество слоев обмотки,

m – реальное количество слоев обмотки,

n – количество элементарных жил в «литцендрате».

Кроме рассмотренных потерь при высокочастотном напряжении в обмотках, необходимо учитывать, что из-за наличия зазоров в сердечнике происходит искривление магнитного поля, что вызывает дополнительные вихревые токи в проводниках